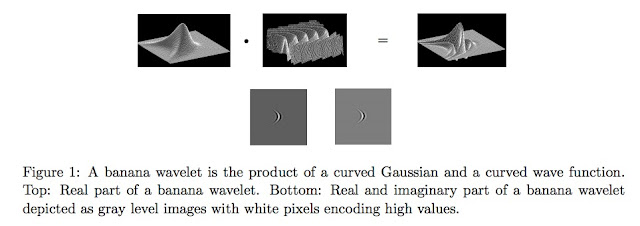
Banana Wavelets

 Time to fire up the wayback machine once again, and take a look at a fascinating wavelet representation apparently lost to the annuls of time. Let's take a look at the classic 'banana wavelet'.

All of this is from the paper titled 'Learning Object Representations by Clustering Banana Wavelet Responses by Peters and Kruger', which you can find here.

A banana wavelet is composed of the product of a warped gaussian and a curved wave function.


We have discussed both scale space pyramids as well as oriented steerable filters recently. So you can now view this banana wavelet through that lens. You can build this beast with different orientations, as shown below.


The mobius topology thing above might seem confusing, but if you think about how you have to compute distance between points in an orientation space, it should start to make sense.  If you are still confused, think about hue distance in a colorspace with a hue axis. Angle has the same modulo property.

So now of course you can immediately recontextualize this whole approach, and use it to construct an oriented banana wavelet scale space pyramid if you so wish.  Have fun.

Comments

Post a Comment

Popular posts from this blog

CycleGAN: a GAN architecture for learning unpaired image to image transformations

Image
 Like the Doublemint Twins touting the joys of Doublemint gum, 2 GANs are surely better than 1 GAN.  Especially if we package them together inside of one meta GAN module.  And this is exactly what the CycleGAN architecture does. Have you ever harbored dark secrets of turning a horse into a zebra?  The CycleGAN was developed to do just that. Learn how to turn a horse into a zebra.  And more. Now right away you can notice a difference between the image to image transformation GAN architectures we've been discussing over the last few posts.  Those last few posts described systems that learn from a database of matched input-output image pairs. And if your goal is to turn an edge representation into a nicely filled in continuous tone image, it's easy to build your database of matched input-output image pairs that your GAN system can then learn off of.  Take a continuous tone image (which will be the output of the database pair entry), then run it through an edge detector algorithm. 
Read more

Pix2Pix: a GAN architecture for image to image transformation

Image
 I thought following up yesterday's TraVelGAN post with a Pix2Pix GAN post would be useful to compare what is going on in the 2 architectures.  Two different approaches to the same problem. I stole this Pix2Pix Overview slide below from an excellent deeplearning.ai GAN course (note that they borrowed it from the original paper) because it gives you a good feel for what is going on inside of the Pix2Pix architecture.    Note how the Generator part is very much like an auto-encoder architecture, but rebuilt using the U-Net architecture features (based on skip-connections) that fastai has been discussing in their courses for several years before it became more widely known to the deep learning community at large  (and which originally came from an obscure medical image segmentation paper) . So the Generator in this Pix2Pix GAN is really pretty sophisticated, consisting of a whole image to image auto-encoder network with U-Net skip connections to generate better image quality at highe
Read more

Smart Fabrics

Image
"What makes smart fabrics revolutionary is that they have the ability to do many things that traditional fabrics cannot, including communicate, transform, conduct energy and even grow."  This is a quote from Rebeccah Pailes-Friedman, who is a professor at Pratt with a research focus on developing wearable technology and smart textiles. Enhancing textiles can be viewed through different lens.  Enhancements can be aesthetic, or performance boosting, or durability boosting. 
Read more