Convex Optimization on Manifolds
Today's lecture is a talk by Richard Hartley presented at Microsoft Research in 2016 that is a good overview of various useful concepts associated with convex manifold optimization.
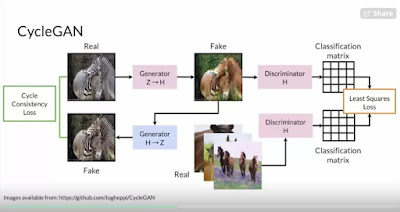
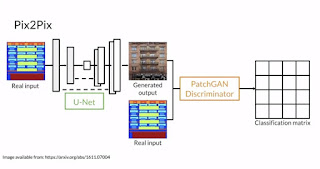
Richard reviews different concepts associated with the structure of convex manifolds, including optimization on a manifold surface, computations on the geodesics of a manifold, Lie group S03 manifolds for 3D rotations, L1 averaging of S03, as well as their application to computer vision problems like structure from motion and hand-eye coordination.
The quaternion representation of rotations is also discussed.
Observations
1: If all rotations in 3D space can be represented on a manifold, what does that tell us about human perceptual representations of 3D objects?
2: Averaging vs Ransac for estimating camera orientation.

Comments
Post a Comment