HTC Seminar Series #36: Mathematical Mysteries of Deep Neural Networks
Today's HTC Seminar Series presentation is a lecture by Stephane Mallat at the ICTP Colloquium recorded in November 2020. He cuts through the BS and gets to the real meat of what is going on under the hood in deep learning neural nets.
ABSTRACT: Deep neural networks obtain impressive results for image, sound and language recognition or to address complex problems in physics. They are partly responsible of the renewal of artificial intelligence. Yet, we do not understand why they can work so well and why they fail sometimes, which raises many problems of robustness and explainability.
Observations:
1: Today's lecture really does give you the keys to the deep learning kingdom. Too bad it has only 1600 views. The rest of the world's loss, and your gain.
2: Think about what he is saying and how it relates to group theory and perceptual manifolds.
3: Something that might be missing from this approach is a data augmentation fold in. Data augmentation is really a key component of deep learning on conventional CNN architectures. How does the concept fit in here?
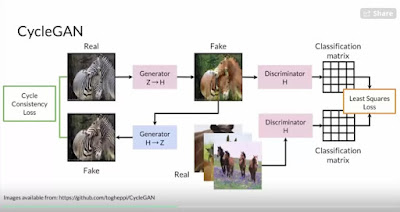
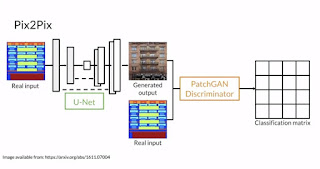

Comments
Post a Comment